lsm-tree
文章内容基于原论文,结合自己的理解和思考,发现有错漏的地方,欢迎反馈探讨,感谢。
LSM-Tree 拥有优异的性能出现在各种存储引擎中,本文希望对 LSM-Tree 进行一个最小全局认识,对其有个骨架结构认识,从 LSM-Tree 的原始论文开始,到现在的进展以及 LSM-Tree 中各种影响的因素。
起始
1 LSM-Tree 的缘起
LSM-Tree 从论文[1] 中出生,在该论文中谈及了 LSM-Tree 诞生的原因,主要流程,优缺点,适合场景,以及决定性能的相关参数等。首先接下来重点介绍这篇 LSM-Tree 的原始论文。
在论文[1] 之前的年代中,存储引擎主要使用 B-Tree 系列的数据结构,这种数据结构并不是 I/O 友好型的,随机 I/O 所带来的成本会比较高,尤其是写多读少的情况下,更新叶子节点会有两次随机 I/O(读+写),会有性能瓶颈。LSM-Tree 则以两个 batch 操作来优化 I/O 成本:1)首先写入 memory,然后 memory 的数据以 batch 形式写入磁盘;2)磁盘顺序读写,减少 seek 的成本(次数减少),均摊后单次成本更低。
由论文[2] 中的结论可知,在一定范围内使用内存换 I/O 能减少整体成本。随着硬件的更新换代,内存和磁盘的成本关系也在变化,可根据具体使用的硬件进行对比。
2 LSM-Tree 的结构,以及主要流程
LSM-Tree 是一个多层的数据结构,其中第一层(最上层)保持在内存中,除第一层外的其他层均在磁盘(部分频繁访问的数据会 cache 在内存)。最简单的 LSM-Tree 拥有两层:内存中一层,磁盘中一层。接下来首先以两层 LSM-Tree 介绍相关功能,后续在定量分析过程中,会详细介绍多层 LSM-Tree 结构。
两层 LSM-Tree 的结构如下所示:
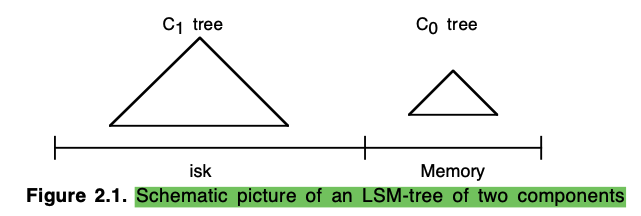
上图中 L0 与 L1 均是 tree-like 的数据结构,由于 L0 不需要特别考虑 tree high(都在内存,无 I/O),因此 B-Tree、AVL-Tree 以及 2-3-tree 等各种 tree like 数据结构读可以。 L1 保存在磁盘,需要考虑 tree high,使用 B-Tree。
对 LSM-Tree 数据结构,首先看一下基本操作的流程(为了描述方便,L0 中的结构也以 B-Tree 为例):
- insert:数据直接写入内存 L0 中。在 L0 大小达到一定阈值后,会进行 rolling merge 操作(后面详述),将数据从 L0 转移到 L1。
- get:读取数据的时候,首先从 L0 中进行查找,找到后直接返回(不管是否带 delete meta 信息的 key/value),否则继续从 L1 进行查找。
- delete:如果 L0 中没有 key/value 对,则在 L0 中增加一个 key/value 对,且 value 包括 delete 相关的 meta 信息;如果 L0 中有对应的 key/value,则将 value 更改为包括 delete meta 信息的值。rolling merge 的时候将带有 delete meta 信息的 key/value 从 L_i 写入到 L_(i+1) 删除 L_i & L_(i + 1) 中的 key/value 对,然后在 L_(i+1) 插入一个带有 delete meta 信息的 key/value 对,当达到最底层的时候,将 key/value 对进行物理删除。同样 delete 的操作和 insert 一样,支持 batch 操作。
- update:update 可以看作是 delete&insert 的组合
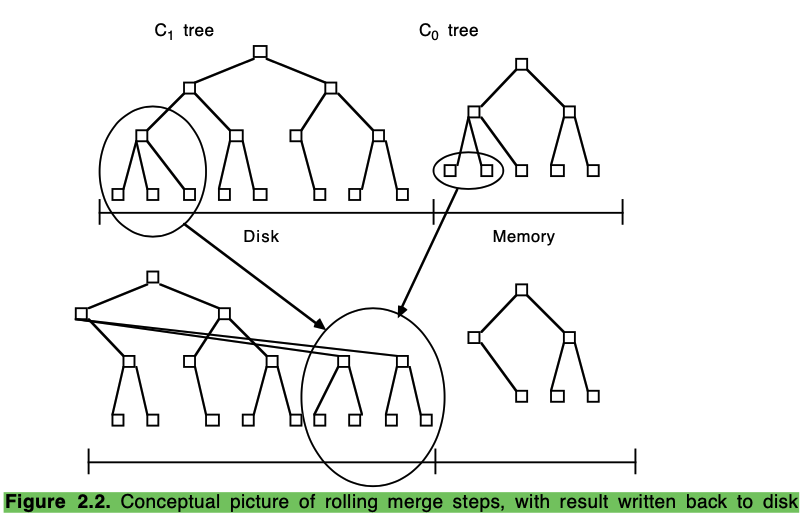
LSM-Tree 为了保证更上层有空间接受插入的新数据,维护一个 rolling merge 的后台流程,该流程会从相邻两层中分别读取数据,写入到下层中,在 rolling merge 的过程中也可以进行部分逻辑处理:比如 ttl 的数据可以直接删除等。下图是一个 rolling merge 的示意图:
3 LSM-Tree 相关的定量分析
上文介绍了 LSM-Tree 诞生的原因,以及基本的流程,下面着重进行性能相关的定量分析,包括双层 LSM-Tree 以及多层 LSM-Tree。
双层 LSM-Tree 的 IO 定量分析
本节介绍双层 LSM-Tree 的 I/O 定量分析,以及和 B-Tree 的相关对比情况。
以下对比内容基于 1995 年的硬件架构:
- 1MByte 内存需要 100$
- 1MByte 磁盘的存储需要 1$
- 随机访问 I/O 成本是 25$
- 顺序访问的 I/O 成本是 2.5$
同时为了后面描述方便,定义变量如下:
- $COST_d$ 表示磁盘存储 1MByte 所需要的成本
- $COST_m $ 表示内存中存储 1MByte 所需要的成本
- $ COST_P $ 表示提供 1 page 每秒所需要的磁盘成本(随机访问)
- $ COST_\pi $ 表示提供 1 page 每秒所需要的磁盘成本(顺序访问)
内存的成本由存储空间决定,而磁盘的成本则由存储空间和访问频率的更大者决定。
假设需要存储 S MByte 大小的数据,且每秒 H 的随机 I/O 访问(数据无缓存),则磁盘的开销是 $ COST_D = max(S COST_d, H COST_P $,其中 $ SCOST_d $ 表示存储所需成本,$ H COST_P $ 则表示随机 I/O 访问的成本。
当使用内存来缓存部分数据后,使得磁盘的瓶颈变为存储量后,则对应总成本是 $ COST-B = S COST_m + SCOST_d $ 其中, $ SCOST_M $ 表示内存的成本,$ SCOST_d $ 表示磁盘的存储所需成本。
综合上面两种情况可得,总共存储 S MByte 大小的数据,且每秒 H 随机访问的总成本公式如下所示:
$ COST-TOT = min(max(SCOST_d, HCOST_P), SCOST_m + SCOST_d) $
通过上述公式我们可以看到,整体的成本受总存储量,以及访问频率的影响,我们将 H/S(访问热度) 作为横轴,COST-TOT 作为纵轴画图得到如下曲线
通过上图可知,总成本会随着访问热度的增长而增长,当达到一定程度后不在增长。上图中两个拐点将数据分为三段:cold,warm,hot。其中第一段的成本主要来源磁盘存储量,第二段则随着访问频率的增加而变多,第三段主要是内存与磁盘容量的成本。其中两个拐点则用如下公式定义
- $ T_f = COST_d / COST_P = 1 / 25 = 0.04 $ 表示 cold 和 warm data 之间的拐点
- $ T_b = COST_m / COST_P = 100 / 25 = 4 $ 表示 warm 和 hot data 之间的拐点
对于连续 I/O 访问来说,也有类似上图的分析,而其中 warm 和 hot 的划分则是对 “The Five Minute Rule”[2] 的概括。
根据论文[3] 中的说法,访问热度与实际的磁盘访问有关,而不是逻辑插入速度,LSM 也是通过减少实际的磁盘访问量来提效,LSM-Tree 有两个减少磁盘访问的点:1)先写内存,然后 batch 写磁盘;2)顺序访问磁盘。接下来接下下顺序 I/O 的收益。
根据[4] 给的数据,随机读取一个磁盘页的耗时大概是 20ms(其中 10ms 用于磁道寻址,8.3ms 来源于旋转延迟,1.7ms 来源实际读取)。顺序读取 64 个磁盘页的耗时大概是 125ms(其中 10ms 来源于磁道寻址,8.3ms 来源于旋转延迟,106.9ms 来源于实际的数据读取),— 平均后大概只需要 2ms 读取一个磁盘页,是随机访问的 1/10。也就是 $ COST_{\pi} / COST_P = \frac{1}{10} $。通过前面计算也能直观感受到顺序 I/O 所带来的(均摊)具巨大性能收益。
我们使用[3] 中的给的结论来计算 “五分钟规则” 的参考区间 — $ \tau $,规则指出“维持每秒 1 page 访问所需要的成本与保存它所需的内存成本一致”,我们得到如下公式
- $ \frac{1}{ \tau } COST_P = pagesize COST_m $ (I/O 速率 * 随机 I/O 的成本 = 内存存储的成本)
那么 $ \tau = (\frac{1}{pagesize} \frac{COST_P}{COST_m}) = \frac{1}{pagesize T_b} $,如果每个 page 是 4k(0.004 Mb) 的话我们可以得到 $\tau = 1/(0.004 * 4) = 62.5 seconds/IO。换句话说在访问间隔小于 62.5 seconds/IO 的时候,用内存换磁盘是合理的(现在需要根据硬件成本进行具体计算)。
B-Tree 和 LSM-Tree 的定量分析对比
在进行 B-Tree 和 LSM-Tree 的对比分析之前,先单独进行 B-Tree 和 LSM-Tree 的分析。主要对比 insert 的性能,同时忽略了 index 更新过程中所带来的微小 I/O 成本。
B-Tree 的定量分析
假设所有的 insert 是完全随机的,因此不会有叶子节点 buffer 在内存的情况。
根据论文[5] 的结论,B-Tree 中的有效深度 - $D_e$ - 表示随机查找中,未在 buffer 中命中的平均 page 数目。在 B-Tree 的插入中,首先需要进行 $D_e$ 次 I/O 查找对应的叶子节点,更新改节点,然后将脏页写回(1 I/O),因此整个 I/O 的开销如下所示
$ COST_{B-ins} = COST_P * (D_e + 1) $
LSM 的定量分析
由于 LSM 的单 entry insert 时直接写入内存,可能没有 I/O 开销,因此分析 LSM-Tree 的 insert I/O 开销时,使用均摊分析进行。
首先定义一些变量如下
- $ S_e $ 表示 entry(index entry) 的大小(byte 为单位)
- $ S_p $ 表示 page size 的大小(byte 为单位)
- $ S_0 $ 表示 C0 中叶子节点的大小(MByte 为单位)
- $ S_1 $ 表示 C1 中叶子节点的大小(MByte 为单位)
- M 表示 rolling merge 的过程中平均有多少个 entry 插入到 每个 C1 的叶子节点 (a given LSM-tree as the average number of entries in the C0 tree inserted into each single page leaf node of the C1 tree during the rolling merge)
每个 page 中的 entry 数目大致为 $ S_p / S_e $,整个 LSM-tree 中在 C0 中的数据比例是 $ S_0 / (S_0 + S_1) $ ),因此 rolling merge 过程中会平均插入到每个 C1 叶子节点的 entry 数 M 可以通过其他公式计算得到 $ M = (S_p/S_e) * (S_0/(S_0 + S_1)) $。
根据上述公式可以得到 LSM-Tree insert 的均摊开销为(将 C1 叶子节点读入和写出内存的开销均摊到 M 个 entry 上)
$ COST_{LSM-ins} = 2 * COST_{\pi} / M $ (读写一次 C1 的叶子节点,平均涉及到 M 个 entry)
对比
观察 B-Tree 和 LSM-Tree 的 insert I/O 开销我们可以得到如下的公式
$ COST_{LSM-ins} / COST_{B-ins} = K1 (COST_{\pi}/COST_{P}) (1 / M) $
其中 $ K1 ~ 2/(D_e + 1) $ 是一个常数
上述公式对比展示出,LSM-Tree 比 B-Tree 的优势主要来自于两方面:1)$COST_{\pi}/COST_{P}$ 也就是磁盘的连续访问相比随机访问所带来的优势;2)M 也就是 rolling merge 时批量写入到 C1 中单个叶子节点的平均 entry 数目(注意 M 并不是一定会大于 1)。
在 B-Tree 作为索引的情况下,如果整体访问热度比较高的话,则可以使用上述公式进行粗略的估算,使用 LSM-Tree 之后大概会有多少收益。
多 component LSM-Tree 的分析
上面所有关于 LSM-Tree 的讨论均假设 LSM-Tree 是两层的,在实际的生成中,LSM-Tree 则可能会有多层,具体的层数,以及相邻层之间的大小比例等可以通过分析得出,本节介绍多层 LSM-Tree 相关的分析。
为了方便讨论,下面的描述中,假设 LSM-Tree 中的 entry 在插入后,仅在最底层进行删除。
上面几节中的分析可以得到从 C0 写入到 C1 每个叶子节点的平均 entry 数目 M 并不一定大于 1,如果 M <= 1 的话,则 LSM-Tree 两个优势中的一个:“批量更新” 就失效了,因此如果分析得知 $ M < K1 * COST_{\pi} / COSTP $ 的话则 B-Treee 比 LSM-Tree 会更好。另外一方面,为了更好的利用 LSM-Tree 的优势,则需要尽可能增大 M(也就是 C0 和 C1 的比值需要更大);同时无限增大 C0 则会由于内存消耗更高造成成本过高,因此需要综合考虑计算一个总成本更小的参数值。
为了保持 LSM-Tree 中上层有空间持续接受新数据,因此 rolling merge 从上层读取并删除的速度与 C0 接受到插入速度需要保持一致。
在两层的 LSM-Tree 中,可以从 LSM-Tree 的总成本出发,寻找更合适的 C0 大小。首先从一个较大的 C0 开始,逐渐减小 C0 的大小(同时 I/O 开销会增加,I/O 的访问频率和存储成本会越来越小),直到达到一个平衡(此情况下再减少 C0 的大小会导致总成本增加)。另外的一个思路则是使用多层的 LSM-Tree 结构(这可以减少 C0 的大小,同时减少 I/O 的访问频率),同时没多一层会多部分 I/O 操作,因此需要综合考虑。
下图是一个多层 LSM-Tree 的结构
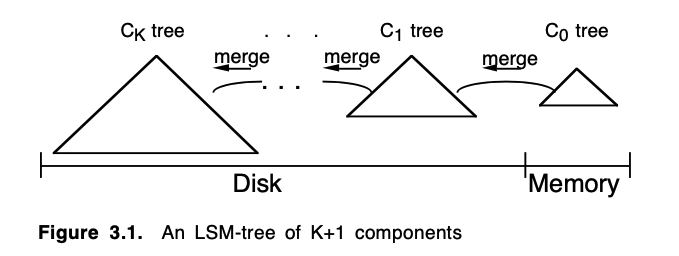
对于 K+1 层的 LSM-Tree 来说,总共有 C0, C1, C2, … C_{K-1} 以及 C_K,并且每层的大小递增(C1 比 C0 大,C2 比 C1 大,依次类推,最小的层 C0 在内存,其他的所有均在磁盘),相邻层之间会有异步的 rolling merge 过程,将 C_{i - 1} 层的数据迁移到 C_i 层中。对于一个插入后从未删除的 entry 来说,会从最上层 C0 逐步迁移到最底层 C_K 中。
接下来会通过定量的分析来说明多层 LSM-Tree 中不同参数对总成本的影响,并且推导得出一个总成本更低的参数组合。
首先定义一些在定量分析中需要的参数与假设
- $ S(C_i) $ — 表示 LSM-Tree 第 i 层叶子层所有 entry 的总大小(单位是 byte)
- $ S_i $ — 表示 LSM-Tree 中第 i 层所有 entry 的总大小(单位是 byte),也就是 $S(C_i) = S_i$
- $ r_i = S_i / S_{i-1} $ — 表示相邻两层中的总大小比例
- S — 表示所有层中叶子节点的总大小,也就是 $S = \sigma{1}{i} S_i$
- R — C0 接受到的插入速度(假设速度相对稳定),单位 byte/s
- 每层的中数据量保持稳定,且接近该层的阈值
- 每个 entry 只从 C0 插入,从 C_K 删除,中间层不删除 entry
- C_K 的大小保持相对恒定,删除与插入保持相对的平衡,C_K 层的删除,可以理解为不增加插入速度的情况下将 entry 从 C_0 删除
假定 LSM-Tree 有 K + 1 层,其中 S_0 和 S_K 固定,S_0 接受到的插入速度 R 恒定
问题:求所有的 $ r_i $ 使得整个 LSM-Tree 的总 I/O 速度 H 最小。
证明过程如下:
- 由于假设每条数据从 C_0 插入后,一直到最底层 C_{K} 才会被删除,则所有相邻层 (C_{i-1}, C_{i}) 的 I/O 速度和 C_0 接受到的 I/O 速度一致,均是 C_0 接受的插入速度 R。
- 如果 C_{i-1} 和 C_{i} 都在磁盘上,那么 C_{i-1} 层从磁盘上读取的 I/O 速度就是 $ R/S_P $(这部分数据会被移入到 $C_{i}$ 层,其中 $S_P$ 是单 page 的字节数大小,从 C_{i} 层会有 $r_i R/S_P$ 的读取 I/O(一个 C_{i-1} 层平均对应 C_{i} 层 r_i 个 page),然后所有读取的数据会写入到 $C_i$ 层,其速度是 $ (r_i + 1) R / S_p $ (从 C_{i-1] 与 C_{i} 读取的数据都会写入到 C_{i} 层中,不会中途删除),因此整个 LSM-Tree 的总 I/O 速度 H 可以用公式计算如下: $ H = (R / S_P) ((2 r_1 + 1) + (2 r_2 + 2) + … + (2r_{K-1} + 2) + (2r_K + 1)). 其中 $ (2 r_i + k) $ 表示 rolling merge 过程中第 i 层的总 I/O 量,其中 $ r_i R / S_p $ 表示从 C_{i-1} merge 到 C_{i} 中从第 i 层读取的 I/O 量,(r_i + 1)R/S_P 表示从 C_{i-1} merge 到 C_{i』 层后写入到第 i 层的 I/O 量,R/S_P 表示从第 i 层 rolling merge 到第 i + 1 层时的读取 I/O (C_0 没有 I/O,C_K 不需要合并到更下一层,没有下一层对应的 I/O)
- 简化 H 后得到 $ H + (R / S_P) ((2 r_1 + 2) + (2 r_2 + 2) + … + (2r_{K-1} + 1) + (2 * r_K + 1)) = (2R/S_p) (\sigma{1}{K} r_i + K - \frac{1}{2}) $
- 需要在已知条件下求 H 的最小值,其中 S_K 和 S_0 恒定,可以换算为同等已知条件 $ \prod\limits_{1}^K r_i = (S_k / S_0) = C $
- 也就是希望在 $ \prod\limits_{1}^K r_i = (S_k / S_0) = C $ 的情况下求 $ \sigma{1}{K} r_i $ 的最小值。
- 通过求偏导,得到 $ 0 = 1 - \frac{1}{r_j} C \prod\limits_{1}^{K-1} r_j^{-1}. 然后求的每个 r_j 等于 $ C * \prod\limits_{1}^{K-1} r_j^{-1} $ 或者 $ C^{\frac{1}/{K}} $ 情况下求的最小值。
- 在 LSM-Tree 中,相邻层然后把条件放宽(也就是不固定最大层的大小),每一层是上一层的 r 倍,由于正常情况下 r 会比较大,因此最大层会占据所有数据的大头(S_K ~~ S),那么固定整体大小 S 和 固定 S_K 就近似(上面的推导过程)
其中通过求偏导得到最小值的过程,自己推导的结果与论文中有差异,如果有人知道,恳请告知,自己推导的结果是 $ 0 = -\frac{1}{r_j} C \prod\limits_{1}^{K-1} r_j^{-1} $ 不是论文中的 $ 0 = 1 - \frac{1}{r_j} C \prod\limits_{1}^{K-1} r_j^{-1} $。
根据已知条件与上述证明可得
- $ S = S_0 + r S_0 + r^2 S_0 + … + r^K * S_0 $
- $ H = (2R / S_p)(K (1 + r) - 1/ 2) — 其中 R 是插入速度,S_p 是页大小,K 是磁盘上的层数,r 是相邻层的比值大小
也就是 R 和 S_K 均保持不变的情况下,H 于 S_0 负相关(内存大小),与 r (相邻层的大小比例)正相关。
可以使用两层 LSM-Tree 进行具体的推演1
2
3
4
5
6
7
8
9两层的 LSM-Tree 中
- K = 1, r = S_1 / S_0
- H = \frac{2R}{S_P}(K*(1+r) - \frac{1}{2})
- COST_tot = COST_m * S_0 + max(COST_d * S_1, COST_\pi * H)
- s = (COST_m * S_0) / (COST_d * S_1) -- cost of memory relative to storage cost for S_1 data
- t = 2 ((R/S_p) / S_1) * (COST_\pi /COST_d) * (COST_m / COST_d)
- C = COST_tot / (COST_d * S_1)
当 S_0 / S1 比较小的时候, C ~ s + max(1, t/s)
其中 C 是 t 和 s 的函数,其中 t 是应用的平均访问热度(the variable t is a kind of normalized temperature measuring the basic multi-page block I/O rate required by the application),s 表示使用的内存大小。
最简单的来说,可以让 s = t, 这样 C = s + 1,这样磁盘得到充分利用(I/O 的存储和访问量都打满)。
个人理解这里是假定总存储量(磁盘所需空间)已知,且访问热度已知,也就是说 C 的最小值就是总成本的最小值。
对于 t < 1 的情况,s = t 的成本是最小的,但是 t > 1 的情况下,C 在 s = t^{1/2} 的时候取得最小值,也就是 C = 2s = 2 t^{1/2}. 这个情况下 COST_tot = 2[(COST_mS_1) (2COST_\piR/S_p)]^{1/2}(通过 C = 2t^{1/2} 以及 C = COST_tot / (COST_d S_1) 然后换算得到),也就是说当 t > 1 的时候(两层的 LSM-Tree 最小代价如前所是),整体代价来源于两方面:1)内存的开销;2)I/O 访问的开销(由于 t 足够高,因此 I/O 开销比 I/O 存储代价更大)
对于 t <= 1 的情况来说,C = s + 1 = t + 1 <= 2. 也就是说总在成本总是小于存储成本的两倍,因此通过存储需求来确定磁盘使用大小,然后利用所有的 I/O 能力来最小化内存使用。(尽可能打满对应存储所能提供的 I/O)
具体例子计算 B-Tree 和 LSM-Tree 的成本分析
上面对 LSM-Tree 和 B-Tree 做了定量分析,接下来使用具体例子计算 B-Tree 和 LSM-Tree 在具体场景下的成本对比。
1 给定如下场景,计算 B-Tree 以及两层 LSM-Tree 的成本
- R = 16000 byte(每个 entry 16 byte,也就是 1000 个 entry 每秒)
- 总共 576 million entries(总存储空间 9.2Gbyte),每个 entry 的 ttl 是 20 days
如果使用 B-Tree 的话,成本如下
- 由于 I/O 访问是瓶颈,因此需要更多的磁盘存储空间才能满足对应的 I/O 访问(H = 2 1000 = 2000 随机访问),COST_P = 25$,那么随机访问的成本是 2000 25$ = 50,000$
- 然后非叶子节点需要缓存,具体的缓存成本计算如下
- 假设叶子节点 70% 满,也就是每个叶子节点有 0.7 * (4K / 16) = 180 个 entry,上层节点需要 576 million/180 = 3.2 million 数据,在加上部分前缀压缩的技术后,假设每个非叶子节点可以存储 200 条数据,也就是 3.2 million / 200 = 16000 个节点,每个 4KB,总共有 64MB 的内存存储空间
- 64MB 的存储空间总成本是 64MB * 100$/MB = 6400 $
- 忽略其他一些细小的成本开销
- B-Tree 的总成本 = 50000$ + 6400$ = 56400 $
两层 LSM-Tree 的话,成本如下
- 首先 C1 需要的总存储空间是 9.2Gbyte,总成本是 .1$/Mbyte * 92000Mbyte = 9200$
- 根据 C1 的大小计算出打满情况下的 H = 92000 / COST_\pi = 9200 / 2.5 ~ 3700 page/s
- 假设单 page 大小 4K 的情况下,根据 H 以及 H = (2R/S_P)(K*(1 + r) - 1/2) 计算得到 r ~ 460,可以得到 C_0 = C_1/460 = 9.2G / 460 = 20Mb
- 20Mbyte C_0 的成本是 20MB * 100$/MB = 2000$,另外增加 2MB 用于 rolling merge 时使用,也就是 2000$ + 200$ = 2200$
- 总成本是 9200 + 2200 = 11400$
大致计算之后 LSM-Tree 比 B-Tree 的成本会低很多(11400 VS 56400),相当于 B-Tree 的 1/5 左右
2 如果 R 增加 10 倍,也就是 160000 byte/s,再计算 B-Tree,两层 LSM-Tree 以及三层 LSM-Tree 的成本
- R = 160000 byte(单 entry 16 byte,也就是 10000 entry/s)
- 576 million entries(总存储量 9.2GByte),每个 entry 的 ttl 是 20 days
B-Tree 的情况下
- 需要使用更多的磁盘来满足相应需求(主要是为了满足 I/O 的读写) 随机访问的总成本是 (2 (160000 / 16)) 25$ = 500,000$(相当于 500G 的存储,实际只需要 9.2G,也就是有 491G 的存储浪费)
- buffer 非叶子节点的成本不变,也就是 6400$
- 总成本 = 500,000$ + 6400$ = 506400$
两层 LSM-Tree 的情况
- 首先通过 t 的公式计算得到 t = 2((R/S_p)/S_1)(COST_\pi/COST_d)*(COST_m/COST_d) ~ 2.2 > 1
- 通过公式得到最低成本 = 2[(COST_mS_1) (2COST_\piR/S_p)]^{1/2} ~ 27129$,其中一半用于磁盘,一半用于内存开销,磁盘的总存储空间是 13.5G(27129/2/1 Mb),135M 的内存
- 额外增加 2M 的内存用于 merge,200$
- 总成本 ~ 27329$
对于三层 LSM-Tree 的情况
- C_2 需要 9.2G 存储,总成本 9.210001$/Mb =9200$, 能提供的 I/O 访问频率 H = 9.2 * 1000 / 2.5 ~ 3700
- 根据 H = (2R/S_p)*(K ( 1 + r) - 1/2) 计算得到 r ~ 23
- C_0 = C_2 / r / r ~ 17MB,成本为 17 * 100$/Mb = 1700$
- C_1 的成本是 C_2 的 1/r = 1/23 也就是 9200/23 * 1$/Mb = 400$ (由于是最大层成本的 1/23,因此在估算时也可以忽略)
- 另外增加 4MB 用于 rolling merge,也就是 400$
- 总成本 ~ 9200$ + 1700$ + 400$ + 400$ = 11700$
对比可知 三层 LSM 的成本(11700$) < 两层 LSM 的成本(27329$) < B-Tree 的成本(506400$)
4 未来可能的优化
- 为了更好的平衡插入和查询性能,留取部分 I/O 供查询使用;另外在 rolling merge 的时候,可以适当保留部分上层数据(并不完全迁移)
- 插入/合并的时候,CPU 做隔离,使用单独的 CPU 做合并,以及 LSM-Tree 结构的维护,这样可以在基本不增加延迟的情况下完成查找。
Ref
[1] The Log-Structured Merge-Tree (LSM-Tree)
[2] The Five Minute Rule
[3] Database Buffer and Disk Configuring and the Battle of the Bottlenecks
[4] GPD Performance Evaluation Lab Database 2 Version 2 Utility Analysis, IBM Document Number GG09-1031-0, September 28, 1989